베이지안 모델링의 기본
이 게시물은 책 [Bayesian Analysis with Python - 2nd , Packt] 을 참고하여 작성되었음을 밝힙니다.
베이지안 통계학은 Bayes' Theorem 을 기반으로 발전한 통계 학문으로
결론부터 이야기 하자면, '우리의 데이터는 알 수 없는 모수를 갖는 확률 분포로 부터 얻어졌다'고 가정하는 것이다.
예를 들어, '동전 던지기' (Coin-flipping) 문제를 생각 해보자.
동전의 앞면을 Head (H) , 뒷면을 Tail (T)라고 한다면 $n$번 동전을 던졌을 때, H가 나올 횟수를 $y$라고 하자.
그렇다면 우리는 자연스럽게 $y$의 확률 분포를 Binomial distribution으로 설정할 수 있다.
$y|\theta \sim Bin(n,\theta)$
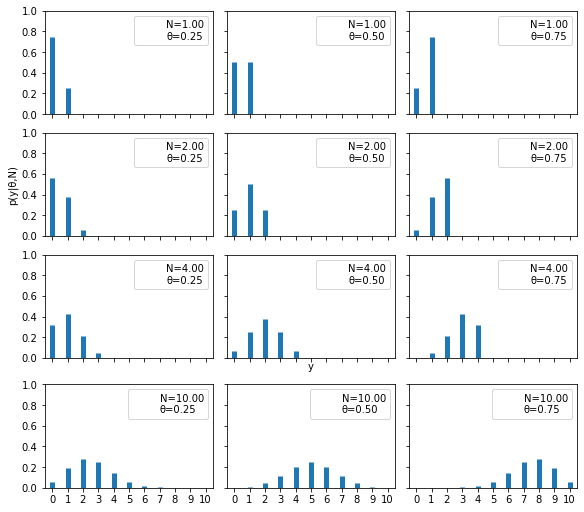
위 그림은 다양한 파라미터 조합에 대한 Binomial distribution의 그래프를 그려본 것이다.
Binomial 분포를 이해하기 위한 참고 그림..
여기서 $\theta$는 동전의 앞면이 나올 확률을 나타낸다.
아마도 일반적으로 우리는 동전의 앞면이 나올 확률을 묻는다면 $ \cfrac{1}{2}=0.5$라고 말할 것이다.
하지만 만약,,,, 동전을 만드는 공장의 공정 과정에 문제가 생겨서 동전의 앞 뒷면 무게가 다르다면?!
아니면 동전을 주머니에 넣고있다가 동전이 살짝 휘어버렸다면?! (피식)
이때도 우리는 여전히 앞면이 나올 확률이 $ \cfrac{1}{2}$ 라고 할 수 있을까?
아마도 이러한 상황에선 앞면이 나올 확률 $\theta$를 '정확히 모르는 값'이라고 두는게 더 합리적일 것이다.
베이지안 학문에서는 데이터에 대한 파라미터 ($\theta$) 를 단순히 '모르는 어떤 값'(Fixed unknown parameter) 으로 보는 것에서 더 나아가 Random Variable이라고 생각한다.
여기서 베이지안 학문의 가장 핵심적인 아이디어를 알 수 있다. 바로, 파라미터 $\theta$의 분포가 존재한다는 것이다.
(왜냐? $\theta$는 Random Variable이니까!)
$\theta$에 대한 분포는 크게 2가지가 있다.
- 데이터 $y$를 관측 하기 이전에, $theta$에 대한 사전 지식 정보를 담은 사전 분포 : Prior distribution $p(\theta)$
- 데이터 $y$를 관측 한 이후, 데이터와 사전 분포을 이용해 계산 되는 사후 분포 : Posterior distribution $p(\theta|y)$
사전 분포는 실험 설계자의 판단으로 설정하게 된다. 보통 이 과정에서 설계자의 주관이 개입되기 때문에 그것에 대한 비난을 받곤 하지만, 그것을 극복하기 위한 여러 방법이 연구되고 있다.
* 사전 분포의 종류만을 주제로 한번 더 포스팅을 할 계획이다.
사후 분포는 베이즈 정리(Bayes' Theorem)를 사용하여 계산 된다.
$$p(\theta|y)=\cfrac{p(y|\theta)p(\theta)}{p(y)}$$
여기서 $p(y)$는 evidence 혹은 normalizing constant 라고도 불리며 $\int p(\theta,y) d\theta$를 계산하여 얻어지는 marginal density이다.
데이터 $y$의 marginal density는 보통 복잡한 적분 계산을 요구하기 때문에 proportional 하게 drop하여 사후 분포를 얻기도 한다.
$$p(\theta|y) \propto p(y|\theta)p(\theta)$$
(처음 베이지안 공부를 하기 시작했을 땐,, 사후 분포를 구할 땐 항상 proportial to 해도 되는 줄 알았는데,, 항상 저렇게 할 수 있는 건 아니었다.. 간혹 우리가 켤레 사전분포를 사용하는 등해서 사후 분포의 꼴을 짐작할 수 있을 때만 proportial 하게 drop하여 계산이 가능한 것이다../ 굳이 normalizing constant를 계산할 필요가 없기 때문에.. 그 외에 경우에선 계산이 필요하다.)
다시 동전 던지기 문제로 돌아오자.
여기서 앞면이 나올 확률 $\theta$에 대한 사전 분포를 $Beta(\alpha,\beta)$ 로 설정하자.
이때 사전분포를 결정하는 모수를 하이퍼 파라미터 (Hyper parameter) 라고 한다.
아래는 다양한 하이퍼 파라미터에 따른 사전 분포 그래프를 그려 본 것 이다.

($\theta$는 확률이기 때문에 갖을 수 있는 값의 범위가 [0,1]이다. 따라서 해당 범위를 만족하는 standard distribution인 Beta distribution을 사전 분포로 설정한다. 또한 베타 분포는 Binomial distribuion의 확률 $\theta$ 에 대한 켤레 사전 분포(Conjugate prior distribution) 이다.)
$\theta$ 에 대한 사후 분포를 계산해 보면,
$ p(\theta)\propto p(y|\theta)p(\theta)$
$={n \choose y} \theta^{y}(1-\theta)^{n-y} \times \cfrac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}\theta^{\alpha-1}(1-\theta)^{\beta-1}$
$\propto \theta^{\alpha+y-1}(1-\theta)^{n+\beta-y-1}$
$\therefore \theta|y \sim Beta(\alpha+y,n+\beta-y)$
이렇게 우리는 데이터가 주어져 있을 때 $\theta$에 대한 사후 분포를 구했다.
이쯤에서 우리는 한가지 의문점을 갖을 수 있다.
'그래서 앞면이 나올 확률이 얼마라는 건데?'
베이지안에서 point estimator로 사용할 수 있는 수치는 많지만 가장 많이 사용되는 수치는 사후 최빈값 (posterior mode) 와 사후 평균 (posterior mean) 이다.
- 사후 최빈값 : $\hat{\theta}=\arg\max_{\theta}p(\theta|y)$
- 사후 평균 : $\hat{\theta}=E[\theta|y]$
보통 Posterior MSE의 관점에서 보면 사후 평균을 파라미터의 점 추정 값으로 가장 많이 사용한다.
이와 관련된 내용 역시 나중에 따로 포스팅을 할 계획 이다.
이 동전 던지기 문제에서는 사후 평균을 확률에 대한 점 추정값으로 사용해보자
그렇다면 우리의 점 추정 값은 아래와 같다!
$$\hat{\theta}=\cfrac{\alpha+y}{\alpha+\beta+n}$$
만약 $\theta$의 사전 분포를 $Beta(1,1)$로 설정하고, 우리가 동전을 10번 던졌고, 총 7번의 앞면이 나왔다면,
우리의 확률 추정 값은 $\hat{\theta}=\cfrac{1+7}{1+1+10}=0.667$ 으로 구할 수 있다.
우리의 사후 추정 값은 Frequentist 들의 일반적인 추정량 MLE : $\cfrac{y}{n}$과 달리 우리의 관측값이 같아도, 사전 분포 설정을 달리 하면 다른 점 추정 값을 얻게 된다.

위 그래프는 3가지의 다른 prior 분포와 9가지의 다양한 데이터에 대한 posterior 분포의 변화를 그래프로 나타낸 것이다.
가장 위의 그래프가 3개의 서로 다른 prior distribution을 나타낸다.
파란색은 $Unif(0,1)=Beta(1,1)$, 오렌지 색은 $Beta(20,20)$ 마지막으로 초록색은 $Beta(1,4)$ 분포를 나타낸다.
아래 9개의 그래프는 레전드안에 데이터가 주어져있을 때, 각각 prior와 데이터에 따른 posterior 분포를 나타낸다.
그래프를 보면 데이터의 trial 횟수 $n$이 작으면 Posterior distribution이 prior distribution에 의해 영향을 많이 받는 것을 알 수 있지만, $n=150$일 때를 보면 Posterior distribution이 prior distribution 와는 거의 상관없이 비슷한 분포를 이루고 있다는 걸 알 수 있다.
오늘은 베이지안 분석의 가장 기본 구조?와 아주 간단한 예제를 살펴 보았다.
다음에는 이 게시물에서 건너뛴 좀 더 상세한 개념들을 차근차근 정리 해보도록 하겠다.