세미나 일시 : 2020년 07월 16일
논문 제목 : BAYESIAN INFERENCE FOR ZERO-INFLATED POISSON REGRESSION MODELS
저자 : HUI LIU and DANIEL A. POWERS
1. 등장 배경
- 보통 count data에 대한 분석을 시행할 때면 poisson model을 적용하는 것이 일반적이지만, 실제 데이터들은 poisson
distribution의 기본가정을 만족하지 않는 것이 일반적이다. $$E[Y] \not = V(Y) $$
ZIP model은 그 중에서도 Zero-inflated count data를 다루기 위해 등장한 모형이다.
Zero-inflated count data는 예를 들어, 우리의 Event가 "지난 한달 동안 응급실에 방문한 횟수" 라고 했을 때, 대부분의 사람들은 방문 횟수가 0일 것이다. 때문에,
observed data에 지나치게 0의 비율이 높을 것이고, 일반 poisson model을 적용하기에 적절하지 않게 된다. 이러한 데이터를 Zero-inflated count data (영과잉 자료) 라고 한다.
2. Classical strategies ( Mixture Distribution for Zero - inflated Count data)
- Zero-inflated data 를 다루는 가장 쉬운 방법은 bernouii-poisson Mixture model을 고려하는 것이다. (Poisson 뿐만 아니라 Negative binomial 과 같은 분포를 Mixture로 사용하기도 하지만, bernouii-poisson Mixture가 가장 쉬운 형태라고 한다.)
Mixture Model을 고려하기 전에 먼저 우리의 관측 값(Observed data) Y를 2가지 stage로 나누어 생각한다.
첫번째 stage는 Transition stage ( Bernouii stage ) , 두번째는 Event count stage ( Poisson stage ) 이다. 관측 값 Y가 이 두 stage를 거쳐서 생성된?관측된 것이라고 보는거다.
먼저 Transition stage는 $\mathbf{Y}$ = \( \langle y_{1}, y_{2}, \dots, y_{n}\rangle \) 에서 $Y_{j}=0$ 값들을 확률적으로 Structural Zero와 Sampling Zero로 구분하는 단계이다.
$$ Z=\begin{cases} 1 & inflated~~zero~~(\textit{structural}) \\
0 & Not~~inflated~~zero~~(\textit{Sampling}) \end{cases} \\
\therefore Z \sim bernouii(p)$$
Structural zero란, 말그대로 구조적인 0값이라는 거다.
예를 들어, 우리의 Event가 "운전을 하다가 인명사고를 낼 사건"이라고 할 때, 운전면허가 없는 사람이나 자동차가 없는 사람은 어쩔수 없이 값이 반드시 0일 수 밖에 없는 것처럼, 그런 구조적으로 반드시 0이어야 하는 값들을 나타낸다.
Sampling Zero는 Poisson distribution에서 관측될 수 있는 0값을 나타낸다.
식으로 나타내자면
$$ (Y|Z=1) = 0 \\ (Y|Z=0) \sim Poisson (\lambda) $$
이와 같다.
둘째로 Event count stage는 $Poisson(\lambda)$분포에서 Event를 관측하는 단계이다.
이 두개의 stage를 이용한 Classical Mixure Model은 크게 2가지가 있는데,
- Poisson Hurdle Model 과
- Zero-inflated Poisson Model (ZIP model) 이다.
먼저 Poisson Hurdle Model을 간단하게 언급하자면, 이 모형은 $Y_{j} = 0$ 값들이 모두 Structural Zero라고 설정한다.
따라서 Event count Stage에서는 $Y_{j}>0$인 값들만 관측이 되는 것이다. 이러한 설정 때문에, 흔히들 Poisson Hurdle Model에서 "The event count are truncated at zero" 라는 표현을 사용한다.
이 모형의 pmf는 아래와 같다.
$$f(y|p,\lambda)=\begin{cases}
p & y=0 \\ (1-p)\frac{f(0|\lambda)}{1-F(0|\lambda)} & y>0
\end{cases}$$
ZIP Model은 Hurdle Model과 달리 0값의 source로 Sampling Zero와 Strictural Zero 모두 고려한다. 따라서 모형의 pmf는 아래와 같다.
$$f(y|p,\lambda)=\begin{cases}
p+(1-p)e^{-\lambda} & y=0 \\ (1-p)f(y|\lambda) & y>0
\end{cases}$$
평균과 분산 Double expectation 공식을 사용하면 쉽게 구할 수 있다.
$$E[Y]=(1-p)\lambda ~~~ V(Y)=(1-p)\lambda(1+p\lambda)$$
3. Bayesain inference for ZIP (regression) Model
- 우선, ZIP model에 Bayesian 방법을 적용하기 전에 왜 Bayesian approach가 필요한가에 대해 생각해 볼 필요가 있다.
ZIP model이 개발되던 초기에는 MLE (Maximum likelihood Estimation) 방법을 기반으로 발전하였다.
Sample size가 큰 경우에는 MLE(여기선 ML Estimator)는 Unbiased and efficient estimator 이고 근사적으로 정규분포를 따른다는 장점이 있지만, sample size가 작을 경우 여러가지 MLE의 장점이 보장되지 않는다.
반면, 베이지안 추정치 ( 일반적으로 Posterior Mean, or Median) sample size에 크게 영향받지 않는 reliable한 estimator를 제공한다.
(물론, bayesian 역시 sample size가 작으면 prior distribution에 의한 영향을 많이 받아서 frequentist들에게 비난 받기도 하지만 여기선 넘어가자.)
또한, MLE를 사용할 때 모수 추정의 불확실성을 보완하기 위해 함께 제공되는 Confidence Interval 은 종종 베이지안의 Credible Interval 처럼 잘못 해석되기도 하고, 베이지안의 입장에서 보자면 MLE는 모수의 불확실성을 충분히 고려하고 있다고 보기도 어렵다.
이와 같은 이유로, 이 논문은 ZIP Model에서 MLE를 대신하여 베이지안 접근법을 제안한다.
3-1.Unconditional ZIP model without covariates
- 2.에서 구한 ZIP model의 pmf를 고려하여 $ Y_{j} \sim ZIP(\lambda,p) , Y_{j} is iid sample$ 일 때,
$\mathbf{Y}$의 pdf 는 아래와 같다.
$$f(\textbf{Y}|\lambda,p)=[p+(1-p)e^{-\lambda}]^{k}[(1-p)e^{-\lambda}]^{n-k}\prod_{j=k+1}^{n}\frac{\lambda^{y_j}}{y_j!}$$
여기서 우리의 모수(Parameter)는 $\lambda,p$이다.
Posterior distribution을 구하기 위해선 모수에 대한 Prior distribution을 설정해야하는데,
일반적인 방법으로는 선행 연구를 답습하거나, Conjugate prior를 고르거나, non-informative prior를 고르는 식의 방법이 있는데, Mixture Model에 대해서는 Conjugate prior를 찾기가 쉽지않다.
이 논문에서는 가장 일반적인 형태인 prior를 골랐고, $\lambda$와 $p$가 prior independet임을 가정했다.
$$ f(\lambda) = Gamma(c,d) \\ f(p) = Beta (a,b)$$
$\therefore$ Posterior distribution of $p,\lambda$
$$f(p,\lambda|\textbf{Y}) \propto [p+(1-p)e^{-\lambda}]^{k}[(1-p)e^{-\lambda}]^{n-k}\lambda^{\sum_{j=k+1}^{n}{y_i}}p^{a-1}(1-p)^{b-1}\lambda^{c-1}e^{-\frac{\lambda}{d}}$$
3.2 ZIP regression model with covariates
- Covariates이 존재하는 regression 모형의 경우, Covariates은 양의 무한대와 음의 무한대 사이의 값을 갖을 수 있지만, 우리의 모수는 $0<p<1 , 0<\lambda$ 이기 때문에, 범위를 만족시키기 위해 link function을 사용한다.
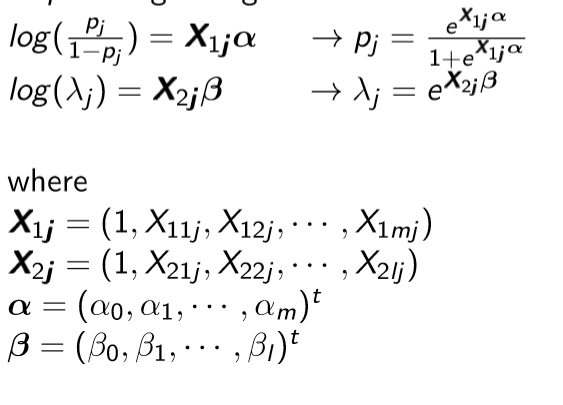
ZIP regression model with covariates의 pdf는 3.1에서 정의 한 식에서 $ p \rightarrow p_{j} , \lambda \rightarrow \lambda_j$ 로 바꿔 대입을 하면된다.
또한, $p_j$와 $\lambda_j $가 위와 같이 정의가 되었기 때문에, 우리의 새로운 모수는 $ \boldsymbol{\alpha,\beta} $가 된다.
( $\boldsymbol{\alpha,\beta}$ 역시 prior independent.)
$$f(\boldsymbol{\alpha,\beta})=\prod_{i=0}^{m}\left(\frac{1}{\sqrt{2\pi}\sigma_{\alpha_i}}e^{-\frac{(\alpha_i-\mu_{\alpha_i})^2}{2\sigma_{\alpha_i}^{2}}}\right)
\prod_{s=0}^{l}\left(\frac{1}{\sqrt{2\pi}\sigma_{\beta_s}}e^{-\frac{(\beta_s-\mu_{\beta_s})^2}{2\sigma_{\beta_s}^{2}}}\right)$$
$\therefore$ Posterior distribution of $\boldsymbol{\alpha,\beta}$
$$f(\boldsymbol{\alpha,\beta}|\textbf{Y,X})\propto f(\textbf{Y}|\boldsymbol{\alpha,\beta,X})f(\boldsymbol{\alpha,\beta}) $$
3.1,3.2의 경우 모두 Joint Posterior distribution을 구했으니 Bayesian 추정을 하기위해 MCMC를 돌리면 되겠다.
각 파라미터들에 대해 Posterior full conditional distribution이 closed form으로 나온다면 Gibbs Sampling을,
그렇지 않다면 M-H algorithm과 같은것을 사용하면 되겠다.
이 논문에서는 Gibbs sampling을 하라고 그 단계를 설명해 놓았던데, 아무래도 통계논문이 아닌 사회과학분야 논문이다보니 실수..?가 있는 것같다. 위와같이 Posterior distribution이 나올 경우, 파라미터들의 conditional distribution은 closed form으로 나오지 않는다. (혹시 나온다면 제게 알려주시길.)
- Full conditional distribution for each parameter.
(1) ZIP model without covariates.
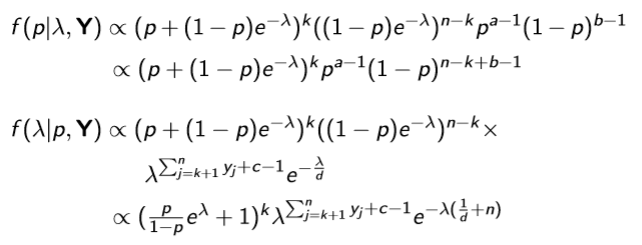
(2) ZIP regression model with covariates.
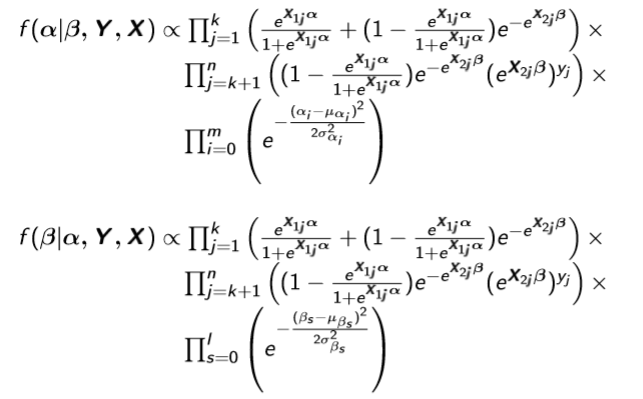
4. Exercise
- 이 논문에선 Americans' changing lives(ACL - Wavve1)데이터를 사용했다고 나와있는데, 동일한 데이터를 구하지 못해서 R로 시물레이션 데이터를 생성해서 간단하게 ZIP Model을 적용해 보았다.
--시나리오
Number of Covariate : $m=l=2$
True value of $\boldsymbol{\alpha}=(-2,0.5,1.2)$
True value of $\boldsymbol{\beta}=(0.3,0.7,0.6)$
-- 이 시나리오를 $n=200$과 $n=1000$ 일 때, 각각 Bayesian 방법과 MLE로 모수를 추정해보았다.
-- Covariates $\boldsymbol{X_{1}},\boldsymbol{X_{2}}$ are generated from $N(0,2),N(0,1)$ each.
(+사실 시뮬레이션을 돌릴때는 사이즈가 $n$인 데이터를 여러개 뽑아서 각각에 데이터 마다 또 MCMC chain도 여러개의 chain을 돌리는게 정석이지만..난 데이터도 한 셋만 뽑고 chain도 parameter당 한개밖에 안돌렸다.
아직 computing 능력이 모자라기 때문이지 ㅎ)
(1) $n=200$,
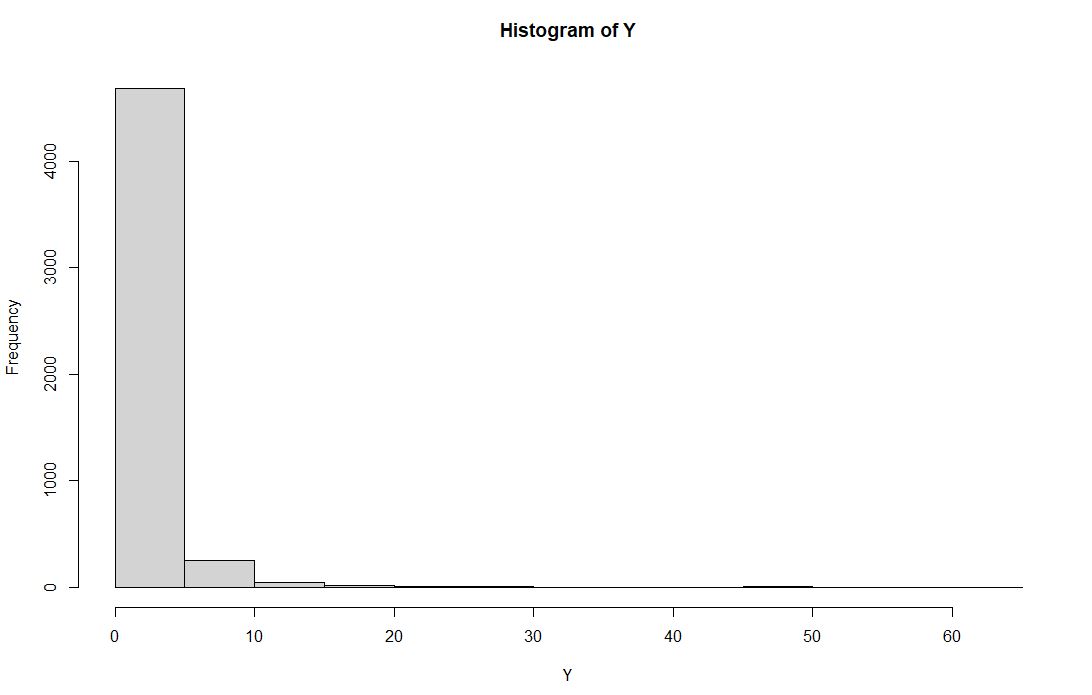
생성한 데이터 $\mathbf{Y}$ 의 histogram , zero proportion : 50.5%
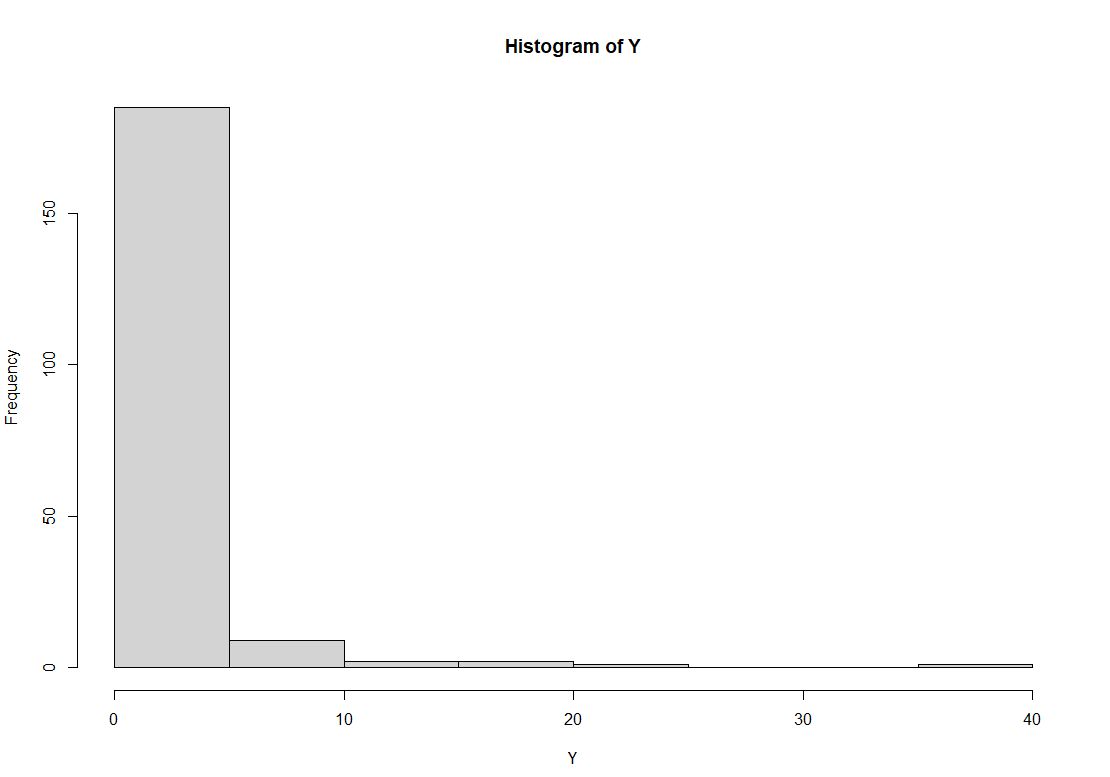
M-H algorithm을 돌리기 위해 설정한 prior distribution은
$\boldsymbol{\alpha} \sim MVN(\textbf{0},1.5I_3)$ , $\boldsymbol{\beta} \sim MVN(\textbf{0},1.5I_3)$이고,
Candidates을 뽑기 위한 proposal densities는 $\boldsymbol{\alpha^{(t)}} \sim MVN(\boldsymbol{\alpha^{(t-1)}},c_aI_3)$ , $\boldsymbol{\beta^{(t)}} \sim MVN(\boldsymbol{\beta^{(t-1)}},c_bI_3)$
여기서 $c_a,c_b$는 scaling factor로 chain의 acceptance rate을 일정한 수준으로 조정하기 위한 factor이다.
여기서는 AR을 0.44정도로 맞추기 위해 매 200번째 iteration마다 AR을 계산하여,
AR<0.44이면 $c/sqrt(2)$ , AR>0.44 이면 $c*sqrt(2)$ 로 factor값을 조정하였다.
초기 값은 $\boldsymbol{\alpha^{(0)}}=(0.1,0.1,0.1), \boldsymbol{\beta^{(0)}}=(0.2,0.2,0.2)$ 로 설정하고
총 Iteration 수 : $T=10000$ , Burn-in period :$t_0=T/2=5000$로 고려하였다.
아래 그림은 Burn-in period를 제외한 Trace plot이다.
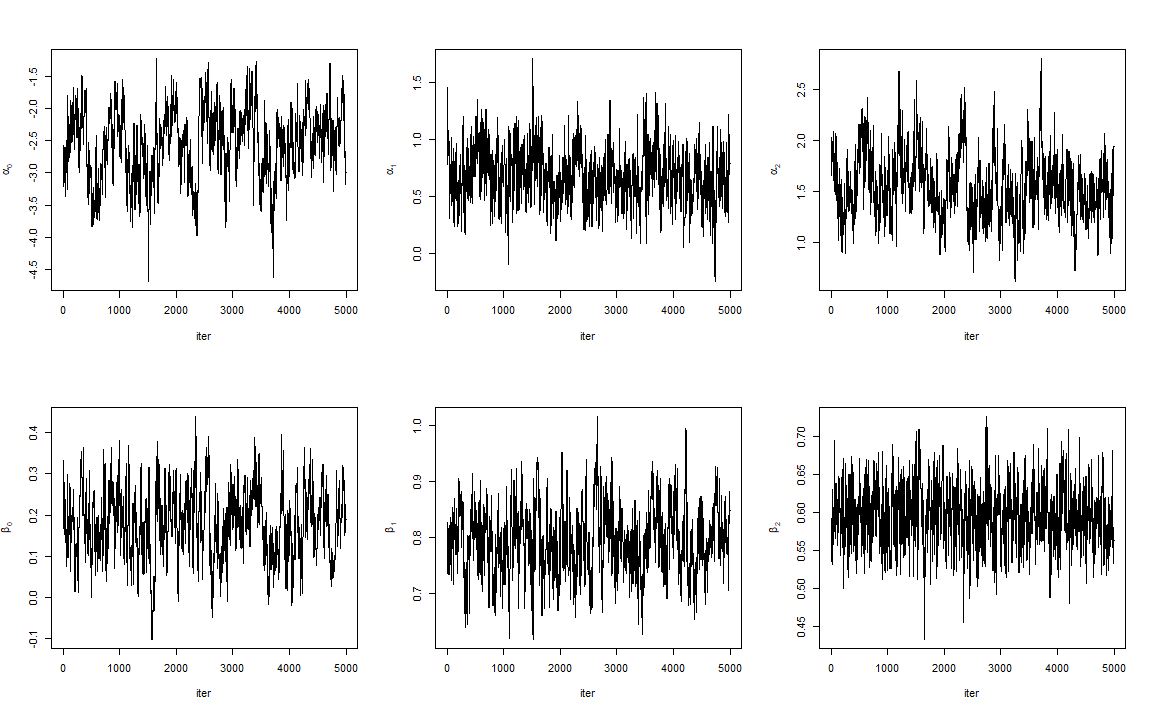
- 음 Trace plot만 보자면 $\beta_2$만 빼고는 다 잘 수렴했다고 판단하기 어려워 보인다.
- 아참, chain 수렴진단은 따로 안했다. 어차피 chain을 각 파라미터들에 대해서 1개씩 밖에 안돌렸기 때문에..
어차피.. 간단하게 해본 예제니까..ㅎ^^ㅎ
MLE는 R "pscl" package 안에 있는 >zeroinfl라는 함수를 사용하여 구했다.
| Method | $\alpha_0$ | $\alpha_1$ | $\alpha_2$ | $\beta_0$ | $\beta_1$ | $\beta_2$ |
| True | -2.0 | 0.5 | 1.2 | 0.3 | 0.7 | 0.6 |
| Bayesian | -2.496 | 0.692 | 1.527 | 0.187 | 0.788 | 0.593 |
| MLE | -4.789 | 1.275 | 2.746 | 0.155 | 0.806 | 0.599 |
결과를 보면, Sample Size가 작아서 MLE는 Bayesian보다 정확하지 못하게 추정된 것을 알 수 있다.
(!! 물론, 이건 하나의 셋을 가지고 한개의 체인만 돌렸기 때문에, 운이 좋은 결과일 수 있다. 여러 데이터 셋을 만들어서 여러개의 체인을 돌리고 그것들의 평균을 estimator로 사용한다면 Bayesian estimator는 True값에 더 근사한 값을 반환할것이다. 혹여나 오해하시는 분들이 있을까..적는다.)
(2) $n=1000$ 일 때, (1)과 동일한 step으로 진행
생성한 데이터 $\mathbf{Y}$ 의 histogram , zero proportion : 48.1%
- Trace Plot (After Burn-in period)
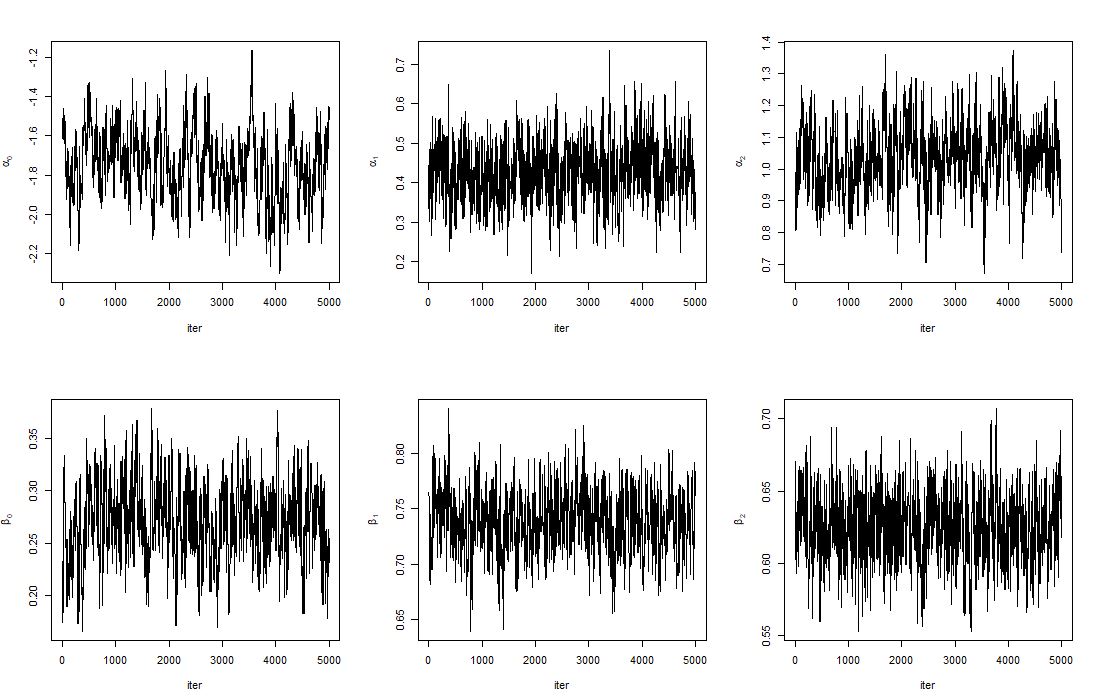
- (1)의 결과보다는 좀 더 잘 수렴한 것처럼 보이는 것 같기도..?
| Method | $\alpha_0$ | $\alpha_1$ | $\alpha_2$ | $\beta_0$ | $\beta_1$ | $\beta_2$ |
| True | -2.0 | 0.5 | 1.2 | 0.3 | 0.7 | 0.6 |
| Bayesian | -1.751 | 0.428 | 1.039 | 0.27 | 0.739 | 0.625 |
| MLE | -1.753 | 0.427 | 1.043 | 0.273 | 0.740 | 0.623 |
- $n$이 커지니, Bayesian과 MLE에 의한 estimators의 값들이 아주 유사해졌다.
5. 결론
- 간단한 예제를 통해, Bayesian이 MLE의 단점을 보완한다는 것을 살펴보았다. ( 사실 이래저래 더 보완할 것이 많지만,)
그런데, 사실 위의 예제 Trace plot을 보면 간단한 Simulation data 임에도 불구하고 chain의 수렴이 잘 이루어지지 않은 것을 알 수 있다. 교수님의 말씀을 빌리자면 ZIP model에서는 chain의 수렴이 잘되지않는 경우가 빈번하고 또한 내가 코드를 짤 때도 iteration이 잘 돌다가 numerical problem 때문에 체인이 중간에 멈추는 등 문제가 발생했었다.
때문에, 이러한 점을 보완할 수 있다면 Bayesian approach를 더 쉽게 사용할 수 있을 것이다.
끝. 다음주에는 더 어려운 논문을 주신다고 하신다.
R-code
#Generate simulation data # Let number of covariates : 2 # m=l=2 n=1000 m=l=2 X1=matrix(1,nrow=n,ncol=(m+1)) X2=matrix(1,nrow=n,ncol=l+1) set.seed(3418) for ( i in 1:n){ X1[i,-1]=rnorm(m,0,2) X2[i,-1]=rnorm(l,0,1) } true.a=matrix(c(-2,0.5,1.2),ncol=3) true.b=matrix(c(0.3,0.7,0.6),ncol=3) p.v=exp(X1%*%t(true.a))/(1+exp(X1%*%t(true.a))) lam.v=exp(X2%*%t(true.b)) Y=c() for (i in 1:n){ Z=rbinom(1,1,prob=p.v[i]) if(Z==1){ Y[i]=0 } else {Y[i]=rpois(1,lam.v[i])} } sum((Y==0))/n par(mfrow=c(1,1)) hist(Y) summary(Y) ##### MLE based ZIP model ##### #install.packages(c("pscl","boot")) library(pscl) library(boot) df.sim=data.frame(Y,X1[,-1],X2[,-1]) colnames(df.sim)=c("Y","X11","X12","X21","X22") mle.zip=zeroinfl(Y~X21+X22|X11+X12,data = df.sim) summary(mle.zip) ##### M-H algorithm ##### #Proposal densities for alpha,beta are N(mean(a_i),1), N(mean(b_s),1) #Prior densities for alpha,beta are N(0,100) k=(Y==0) sum(k) likl.h=function(a,b){ p=(exp(X1%*%t(a))/(1+exp(X1%*%t(a)))) lam=exp(X2%*%t(b)) den=prod(p[k]+(1-p[k])*exp(-lam[k]))*prod((1-p[!k])*lam[!k]^(Y[!k])*exp(-lam[!k])) return(den) } likl.h(true.a,true.b) T=10000 burn.in=T/2 A=matrix(NA,ncol=3,nrow=T) B=matrix(NA,ncol=3,nrow=T) library(mvtnorm) S=diag(3) A[1,]=c(.1,.1,.1) B[1,]=c(.2,.2,.2) c.a=c.b=1 i=1 for ( i in 1:(T-1)){ #Sampling alpha mu.a=A[i,] candi.a=rmvnorm(1,mean=mu.a,sigma=c.a*S) U=runif(1) deno=likl.h(candi.a,matrix(B[i,],ncol=3))*dmvnorm(candi.a,mean = c(0,0,0),sigma = 1.5*diag(3))/dmvnorm(candi.a,mean =mu.a,sigma = c.a*S) nume=likl.h(matrix(A[i,],ncol=3),matrix(B[i,],ncol=3))*dmvnorm(A[i,],mean =c(0,0,0),sigma = 1.5*diag(3))/dmvnorm(A[i,],mean =candi.a,sigma = c.a*S) ar=min(deno/nume,1) if(U<=ar){ A[i+1,]=candi.a }else{A[i+1,]=A[i,]} #Sampling Beta mu.b=B[i,] candi.b=rmvnorm(1,mean =mu.b,sigma=c.b*S) U=runif(1) deno=likl.h(matrix(A[i+1,],ncol=3),candi.b)*dmvnorm(candi.b,mean =c(0,0,0),sigma = 1.5*diag(3))/dmvnorm(candi.b,mean =mu.b,sigma = c.b*S) nume=likl.h(matrix(A[i+1,],ncol=3),matrix(B[i,],ncol=3))*dmvnorm(B[i,],mean =c(0,0,0),sigma = 1.5*diag(3))/dmvnorm(B[i,],mean =candi.b,sigma = c.b*S) ar=min(deno/nume,1) if(U<=ar){ B[i+1,]=candi.b }else{B[i+1,]=B[i,]} #check AR if(i%%200==0){ A.ar=sum(as.numeric(diff(A[(i-199):i,1])!=0))/200 B.ar=sum(as.numeric(diff(B[(i-199):i,1])!=0))/200 if (A.ar<0.44){c.a=c.a/sqrt(2)} if (A.ar>0.44){c.a=c.a*sqrt(2)} if (B.ar<0.44){c.b=c.b/sqrt(2)} if (B.ar>0.44){c.b=c.b*sqrt(2)} } } sum(as.numeric(diff(B[,1])!=0))/T sum(as.numeric(diff(A[,1])!=0))/T sum(as.numeric(diff(B[burn.in:T,1])!=0))/burn.in sum(as.numeric(diff(A[burn.in:T,1])!=0))/burn.in par(mfrow=c(2,3)) plot(A[burn.in:T,1],type="l",ylab=expression(alpha[0]),xlab="iter") plot(A[burn.in:T,2],type="l",ylab=expression(alpha[1]),xlab="iter") plot(A[burn.in:T,3],type="l",ylab=expression(alpha[2]),xlab="iter") plot(B[burn.in:T,1],type="l",ylab=expression(beta[0]),xlab="iter") plot(B[burn.in:T,2],type="l",ylab=expression(beta[1]),xlab="iter") plot(B[burn.in:T,3],type="l",ylab=expression(beta[2]),xlab="iter") a=matrix(colMeans(A[burn.in:T,]),ncol=3) true.a b=matrix(colMeans(B[burn.in:T,]),ncol=3) true.b
'Statistics > 논문 리뷰' 카테고리의 다른 글
| 밀도 기반 군집 방법 - DBSCAN (0) | 2022.03.10 |
|---|---|
| 보조 혼합 샘플링을 이용한 베이지안 로짓 모형(Bayesian logit models with auiliary mixture sampling) (1) | 2022.03.07 |
| Bayesian Analysis of Zero-Inflated regression models (0) | 2021.01.08 |
| ZIP and Binomial regression with Random effect_요약 정리 (0) | 2020.12.28 |




댓글