세미나 일시 : 2020-09-28
논문 제목 : Bayesian Analysis of Zero-Inflated regression models
논문 저자 : Sujit K.Grosh, Pabak Mukhopadhyay, Jye-Chyi Lu
이 논문은 간단하게 요약하자면, 이전 논문들에서 ZIP, ZIB, ZINB 이런식으로 전개했던 여러개의 모형을 ZIPS (Zero inflated Power Series model)로 다시 한번 전개하고 더 나아가 Bayesian approach를 적용한 논문이라고 할 수 있다.
1. ZIPS model
우리가 알고 있는 다양한 standard distribution은 어떤 family로 묶일 수 있다.
(아마 이 문장을 읽고 여러분이 가장 먼저 떠올렸을 것은 바로 exponential famliy ㅋㅋ)
이것과 비슷한 맥락으로 우리는 몇몇 분포들을 Power Series distribution으로 정의할 수 있다.
* 사실 power series distribution이라는 게 정말 family와 같은 의미인지는 정확히 모르겠지만..나는 비슷한 맥락으로 이해하였다.
(https://www.randomservices.org/random/special/PowerSeries.html <- 이 링크로 들어가면, Power Series distribution에 대한 간단한 설명과 예제를 볼 수 있다.)
** ZIP(Zero-Inflated Poisson) 모형에 대한 전개는 이전 게시물을 보시면,,이해에 약간의 도움이 될 수 있을 것입니다
- https://harang3418.tistory.com/2?category=829452
Bayesian Approach for ZIP model _ 정리,예제
세미나 일시 : 2020년 07월 16일 논문 제목 : BAYESIAN INFERENCE FOR ZERO-INFLATED POISSON REGRESSION MODELS 저자 : HUI LIU and DANIEL A. POWERS 1. 등장 배경 - 보통 count data에 대한 분석을 시행할 때면..
harang3418.tistory.com
ZIPS model 정의 :
Let $Y=V(1-B)$
여기서 $V$는 $V \sim PS(\theta)=\frac{b(v)}{c(\theta)}\theta^{v}~,~c(\theta)=\sum_{v=0}^{\infty}b(v)\theta^{v}$,
$B$ 는 $B \sim Bernoulli(p)$
$\therefore E[Y]=(1-B)E(V)~,~V(Y)=\frac{p}{1-p}[E(Y)]^2+\delta E(Y)$
$+ E(V)=\theta(\frac{d}{d\theta}log(c(\theta)))$
(EX) $V\sim Poisson(\theta)$라면, $c(\theta)=e^{\theta}$, $b(v)=\frac{1}{v!}$
$V(Y)$는 약간의 유도과정이 필요하니까 쉽게 유도가 가능하다. $\delta=\frac{V(V)}{E(V)}$
이 $\delta$로 Y의 대략적인 분포를 알 수 있다.
$\rightarrow$ when $\delta \geq 0$ :Distribution of Y is overdispersed.
$\rightarrow$ when $\delta \le 0$ :Distribution of Y is underdispersed if and only if $E(V)\le \frac{1-\delta}{p}$
이 Power series distribution을 이용하여 Likelihood function을 유도하자.
$P(Y=0)=p+(1-p)\frac{b(0)}{c(\theta)}$
$P(Y=k)=(1-p)\frac{b(k)\theta^k}{c(\theta)},~~k=1,2,\cdots$
->
$\begin{split}
L(p,\theta|\boldsymbol{Y})=&\prod_{i=1}^{n}[p+(1-p)\frac{b(0)}{c(\theta)}]^{I(y_i=0)}[(1-p)\frac{b(y_i)\theta^{y_i}}{c(\theta)}]^{I(y_i>0)}\\
\propto&[pc(\theta)+(1-p)b(0)]^{S_0}(1-p)^{n-S_0}\theta^{S}(c(\theta))^{-n}\\
\propto&\left[\sum_{j=0}^{S_0}\omega_{j}p^j(1-p)^{n-j}\right]\theta^S
\end{split}$
where $S_0=\sum I(y_i=0)~~,~S=\sum y_i~~,~\omega_j=\binom{S_0}{j}\left(\frac{b(0)}{c(\theta)}\right)^{n-j}$
- ZIPS model with covariates : Link function을 사용.
Let $\mu$ : mean vector of $V$
$Y_i ~ ind \sim ZIPS(p_i,\theta_i)$ 여기서 $p_i$와 $\theta_i$는 각각 $B_i$와 $V_i$의 distribution parameter
$\Rightarrow log(\boldsymbol{\mu})=\boldsymbol{Z\beta}~,~logit(\boldsymbol{p})=W\gamma$
여기서 $Z~,~W$ 는 각각 function에 대응되는 Covariate matrix이다.
기본적인 모형의 형태는 이와 같다.
만약, Covariate이 없는 ZIPS모형일 경우 Gibbs sampling을 쉽게 활용할 수 있지만, Covariate이 있는 모형의 경우엔 data augmentation을 사용하여 약간의 더 전개가 필요하다.
2. Bayesian Analysis
- Bayesian Approach를 적용하기 전에 앞서 언급했던 data augmentation과정을 진행한다.
우리는 이미 우리의 observed data $Y$를 2개의 latent variables을 사용하여 분해하였다. $Y=(1-B)V$
따라서, 우리는 Gibbs sampling을 Model with covariates에도 적용하기위해 $V,B$의 Conditional density function을 구한다.
▷ Find $P(\boldsymbol{B},\boldsymbol{V}|\boldsymbol{Y},\theta,p)$
이 과정은 수식적으로 이해하려고 하는 것 보단, 의미를 이해하는 것이 더 쉽다.
생각해보자, $Y=(1-B)V$일때, $P(V,B=0|Y)$의 확률은 어떻게 될까?
⊙$V=Y=0$, -> $\frac{(1-p)p(V=0)}{p+(1-p)p(V=0)}$
⊙$V=Y>0$, -> $\frac{(1-p)p(V=v)}{(1-p)p(V=v)}=1$
⊙$V>0~,~Y=0~,~Y\neq V$ -> 0
⊙$V=0~,~Y>0$ -> 0
또 $P(V,B=1|Y)$는 어떻게 될까? $B=1$이면, 반드시 $Y=0$ 이어야 한다.
⊙ $Y=0$ -> $\frac{pP(V=v)}{p+(1-p)P(V=v)}$
이 과정을 다시 정리해 보자면,
For $i=1,\cdots,n$ ,
If $Y_i=0$ - > {$B_i=0\&V=0~,~B_i=1\&V_i\geq0$}
If $Y_i\geq0$ - >{$B_i=0\&V_i>0$}
인 것을 알수 있다. 각각의 확률은 위에서 구해 놓았으니, 해당 확률을 사용하여 $L(p,\theta,\boldsymbol{B},\boldsymbol{V}|\boldsymbol{Y})$ 를 다시 유도하면,
$\begin{split}
L(p,\theta,\boldsymbol{B},\boldsymbol{V}|\boldsymbol{Y})=&\prod_{i=1}^{n}\left(p\frac{\theta^{V_i}b(k)}{c(\theta)}\right)^{B_i}\left((1-p)\frac{\theta^{V_i}b(k)}{c(\theta)}\right)^{1-B_i}\\
=&p^{\sum B_i}(1-p)^{\sum(1-B_i)}\theta^{\sum V_i}[b(k)]^nc(\theta)^{-n}
\end{split}$
이와 같이 정리된다.
여기까지가 data augmentation 과정이구, covariate이 없는 경우에 대해 간단한 예를 들어보면
(ex) $V\sim PS(\theta)=Poisson(\theta)$, $P(p)=beta(b_1,b_2)~,~P(\theta)=gamma(a_1,a_2)$
$\begin{split}
P(p,\theta|\boldsymbol{B},\boldsymbol{V})=&L(p,\theta|\boldsymbol{B},\boldsymbol{V})P(p)P(\theta)\\
=&p^{\sum B_i +b_1-1}(1-p)^{\sum(1-B_i)+b_2-1}\theta^{\sum V_i+a_1-1}e^{-(n+a_2)\theta}
\end{split}$
$\therefore P(p|-)=beta(\sum B_i +b_1,\sum(1-B_i)+b_2)$\\~~~$P(\theta|-)=Gamma(\sum V_i+a_1,n+a_2)$
이렇게 해서 Gibbs sampling을 진행할 수 있게된다.
(그런데 여기서 의문..은 분명히 이 논문에선 with covariate의 경우에도 Gibbs sampling을 할 수 있도록 data augmentation을 쓴다고 했는데, with covariate 부분에서 ARS(Adaptive rejection sampling)를 사용했다.
이 부분은 아직도 해결하지 못한 미스테리다.)
다시 with covariate 으로 돌아와서..
$log(\boldsymbol{\mu})=\boldsymbol{Z\beta}~,~logit(\boldsymbol{p})=W\gamma$
Set prior distribution of $\beta,\gamma$:
$P(\beta)=N_q(\beta_0,\sigma^{2}_{\beta}I_q)~,~P(\gamma)=N_r(\gamma_0,\sigma^{2}_{\gamma}I_r)$
이렇게 설정한 후에 아래와 같이 sampling을 진행한다.

*** ARS는 간단하게 얘기하자면, target density을 여러 구간으로 나눠서 그 구간에 대한 기울기들을 이어서 proposal density를 만드는..그런 방법이다. 나중에 더 공부해서 포스팅 해보도록 하겠다.
3. Simulation Study
이 논문엔 simulation study와 실제 데이터를 사용한 예제가 실려있는데, 실제 데이터를 구해보진 못해서 그냥 simulation study 만 간단히 리뷰하고 글을 마무리 하려고한다.
Simulation study는 without covariates에 대해서 이루어 졌다.
PS($\theta$) 분포로, $Poisson(\theta)$와 $NB(r,\theta)$를 사용한다. $\#~ of~ success~ :~ r$ 도 R.V
Gibbs sampling을 시행 하였고, Chain의 수렴을 판단하기위해 parameters, P(Y=0),$\mu$,Deviance 를 모니터링하였다.
Number of chain : 3
Number of iteration : 10000
Burn-in period : 5000
After burn-in period, every $5^{th}$ sample was kept
$\Rightarrow$ total number of samples : 3000
Simulation :
(1) Y$\sim poisson(\theta)$
Prior : $p(\theta)=Gamma(a1,a2)$
Post : $P(\theta|\boldsymbol{Y})\propto Gamma(\sum_{i=1}^{n}y_i+a1,n+a_2)$}
(2) Y$\sim NB(r,\theta)$
Prior : $p(\theta|r)=Beta(a_1,a_2r+1)~,~p(r)=\frac{1}{15}$
Post : $p(\theta,r|\boldsymbol{Y})\propto p(\boldsymbol{Y}|\theta,r)p(\theta|r)p(r)$
Conditional : $p(\theta|-)\propto Beta(\sum_{i=1}^{n}y_i+a_1,(n+a_2)r+1)$
$p(r|-)=\left[\prod_{i=1}^{n}{y_i+r-1 \choose y_i}\right](1-\theta)^{(n+a_2)r}$
(3) Y$\sim ZIP(p,\theta)$
Prior : $p(\theta)=Gamma(a1,a2)$, $p(p)=Beta(b1,b2)$
Conditional : $p(\theta|-)\propto Gamma(\sum_{i=1}^{n}V_i+a_2,n+a_2)$
$p(p|-)\propto Beta(\sum_{i=1}^{n}B_i+b_1,\sum_{i=1}^{n}(1-B_i)+b_2)$}
(4) Y$\sim ZINB(r,p,\theta)$
Prior : $p(\theta)=Beta(a_1,a_2r+1)~,~p(p)=Beta(b1,b2)~,~p(r)=\frac{1}{15}$
Conditional : $p(\theta|-)\propto Beta(\sum_{i=1}^{n}V_i+a_1,(n+a_2)r+1)$
$p(p|-)\propto Beta(\sum_{i=1}^{n}B_i+b_1,\sum_{i=1}^{n}(1-B_i)+b_2)$
$p(r|-)\propto\left[\prod_{i=1}^{n}{y_i+r-1 \choose y_i}\right](1-\theta)^{(n+a_2)r}$
전체 Sampling 과정 :
$\cdot$ Set initial value : $p^{(1)}~,~\theta^{(1)}~,~r^{(1)}$
$\cdot$ For( j in 1:(N-1)):
for(i in 1:n):
Sampling $B_i~,~V_i$:
IF $Y_i=0$ : Sampling $B_i$ from Bernoulii($p^{(j)}$)
if $B_i=1$ : Sampling $V_i$ from $PS(\theta^{(j)})$
if $B_i=1$ : $V_i=0$
Independent sampling for $r^{(j+1)}$,$r^{*}\sim DiscreteUnif(1,15)$
Gibbs Sampling for $\theta^{(j+1)}$ from $P(\theta|-)$
Gibbs sampling for $p^{(j+1)}$ from $P(p|-)$
시뮬레이션 결과 :

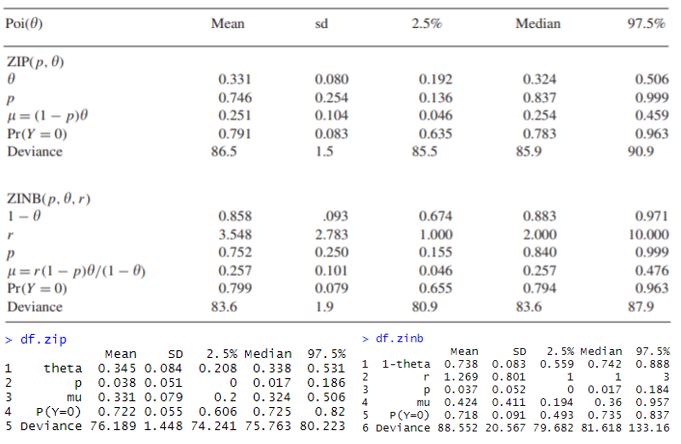
결과를 보면 $Y\sim Poisson$ 인 simulation (1),(3)에 대해서는 내가 돌린 결과가 논문 결과와 유사하게 나왔는데, (2)와 (4)에 대해서는 결과가 좀 다르게 나오는걸 알 수 있다.
아마 무언가 잘못되었다면 $r$이 잘못 sampling이 된 것이 아닐까 싶은데,,,논문 결과가 잘못된게 아닌가 싶기도 하고...
(음모 ㅎㅅㅎ)
**** 글 후반부에 R-code를 첨부해 놓았으니 혹시라도 누군가 오류를 발견한다면 알려주세요!
4. Conclusions
이 논문은 선행 연구 되었던 ZIP,ZINB 모형을 Power Series 를 사용한 모형으로 확장하였고, Bayesian analysis를 사용하여 small sample에 대해서도 효율적으로 작동하는 것을 보였다.
Zero-Inflated model은 count data with many zero 에 대해서 굉장히 useful한 방법이므로 다양한 분야에서 더 많이 연구 될 수 있을 것이다.
R-CODE
library(mcmc) library(MASS) library(coda) library(extraDistr) library(MCMCpack) rm(list=ls()) #4.1 no covariate study ################################################# # use poisson(theta),NB for distribution of V # prior of p : beta(0.5,0.5) # prior of theta : gamma(0.001,0.001) # prior of r : discrete uniform[1,15] Y=c(rep(0,42),rep(1,8),rep(2,2),rep(3,2)) length(Y) #54 sum(Y==0)/length(Y) #= 0.78 num.iter=10000 burn.in=5000 a1=a2=0.001;b1=b2=0.5 n=length(Y) index=seq(5,burn.in,5)+5000 set.seed(3418) ################################################# # Y~poisson sample.1=rgamma(num.iter,shape=sum(Y)+a1,rate=n+a2) sample.1=sample.1[index] sample.2=rgamma(num.iter,shape=sum(Y)+a1,rate=n+a2) sample.2=sample.2[index] sample.3=rgamma(num.iter,shape=sum(Y)+a1,rate=n+a2) sample.3=sample.3[index] sample.case1=c(sample.1,sample.2,sample.3) df.pois=data.frame("X1"=character(),"X1"=numeric(),"X1"=numeric(),"X1"=numeric(),"X1"=numeric(),"X1"=numeric()) #summaries for theta df.pois[1,]=cbind("theta",round(mean(sample.case1),3), round(sd(sample.case1),3), round(quantile(sample.case1,0.025),3), round(quantile(sample.case1,0.5),3), round(quantile(sample.case1,0.975),3)) #summaries for P(Y=0) prob.z=ppois(0,sample.case1) df.pois[2,]=cbind("P(Y=0)",round(mean(prob.z),3), round(sd(prob.z),3), round(quantile(prob.z,0.025),3), round(quantile(prob.z,0.5),3), round(quantile(prob.z,0.975),3)) #summaries for deviance dev.pois=-2*log(exp(-n*sample.case1)*sample.case1^{sum(Y)}/prod(factorial(Y))) df.pois[3,]=cbind("Deviance",round(mean(dev.pois),3), round(sd(dev.pois),3), round(quantile(dev.pois,0.025),3), round(quantile(dev.pois,0.5),3), round(quantile(dev.pois,0.975),3)) colnames(df.pois)=c("","Mean","SD","2.5%","Median","97.5%") df.pois ################################################# ################################################# #2.Y~NB(r,theta) #starting point r = 1,2,3 d.r=function(candi,t){ den=prod(choose(Y+candi-1,Y))*(1-t)^{(n+a2)*candi} return(den) } set.seed(0828) #sample.1 with starting point r=1 r.1=rep(1,num.iter) theta.1=rep(0,num.iter) for ( i in 1:num.iter){ if(i==1){ theta.1[1]=rbeta(1,sum(Y)+a1,(n+a2)*r.1[i]+1) } else{ # Do independet sampling for r candi.r=rdunif(1,1,15) u=runif(1) a=min((d.r(candi.r,theta.1[i-1])/ddunif(candi.r,1,15))/(d.r(r.1[i-1],theta.1[i-1])/ddunif(r.1[i-1],1,15)),1) if(u<=a){r.1[i]=candi.r} else{r.1[i]=r.1[i-1]} # Gibbs sampling for theta theta.1[i]=rbeta(1,sum(Y)+a1,(n+a2)*r.1[i]+1) } } #sample.2 with starting point r=2 r.2=rep(2,num.iter) theta.2=rep(0,num.iter) for ( i in 1:num.iter){ if(i==1){ theta.2[1]=rbeta(1,sum(Y)+a1,(n+a2)*r.2[i]+1) } else{ # Do independet sampling for r candi.r=rdunif(1,1,15) u=runif(1) a=min((d.r(candi.r,theta.2[i-1])/ddunif(candi.r,1,15))/(d.r(r.2[i-1],theta.2[i-1])/ddunif(r.2[i-1],1,15)),1) if(u<=a){r.2[i]=candi.r} else{r.2[i]=r.2[i-1]} # Gibbs sampling for theta theta.2[i]=rbeta(1,sum(Y)+a1,(n+a2)*r.2[i]+1) } } #sample.3 with starting point r=3 r.3=rep(3,num.iter) theta.3=rep(0,num.iter) for ( i in 1:num.iter){ if(i==1){ theta.3[1]=rbeta(1,sum(Y)+a1,(n+a2)*r.3[i]+1) } else{ # Do independet sampling for r candi.r=rdunif(1,1,15) u=runif(1) a=min((d.r(candi.r,theta.3[i-1])/ddunif(candi.r,1,15))/(d.r(r.3[i-1],theta.3[i-1])/ddunif(r.3[i-1],1,15)),1) if(u<=a){r.3[i]=candi.r} else{r.3[i]=r.3[i-1]} # Gibbs sampling for theta theta.3[i]=rbeta(1,sum(Y)+a1,(n+a2)*r.3[i]+1) } } r=c(r.1[index],r.2[index],r.3[index]) theta=c(theta.1[index],theta.2[index],theta.3[index]) df.NB=data.frame("X1"=character(),"X1"=numeric(),"X1"=numeric(),"X1"=numeric(),"X1"=numeric(),"X1"=numeric()) #summaries for 1-theta df.NB[1,]=cbind("1-theta",round(mean(1-theta),3), round(sd(1-theta),3), round(quantile(1-theta,0.025),3), round(quantile(1-theta,0.5),3), round(quantile(1-theta,0.975),3)) #summaries for r df.NB[2,]=cbind("r",round(mean(r),3), round(sd(r),3), round(quantile(r,0.025),3), round(quantile(r,0.5),3), round(quantile(r,0.975),3)) #summaries for mu mu=r*theta/(1-theta) df.NB[3,]=cbind("mu",round(mean(mu),3), round(sd(mu),3), round(quantile(mu,0.025),3), round(quantile(mu,0.5),3), round(quantile(mu,0.975),3)) #summaries for P(Y=0) prob.z=pnbinom(0,r,1-theta) df.NB[4,]=cbind("P(Y=0)",round(mean(prob.z),3), round(sd(prob.z),3), round(quantile(prob.z,0.025),3), round(quantile(prob.z,0.5),3), round(quantile(prob.z,0.975),3)) #summaries for deviance dev.nb=-2*(sum(Y)*log(theta)+n*r*log(1-theta)+sum(as.numeric(Y==0))*log(choose(r-1,0))+ sum(as.numeric(Y==1))*log(choose(r,1))+sum(as.numeric(Y==2))*log(choose(r+1,2))+ sum(as.numeric(Y==3))*log(choose(r+2,3))) df.NB[5,]=cbind("Deviance",round(mean(dev.nb),3), round(sd(dev.nb),3), round(quantile(dev.nb,0.025),3), round(quantile(dev.nb,0.5),3), round(quantile(dev.nb,0.975),3)) colnames(df.NB)=c("","Mean","SD","2.5%","Median","97.5%") df.NB ################################################# #3.Y~ZIP(p,theta) ################### set.seed(0828) # starting p=0.3/ theta = 1 p.1=rep(0.3,num.iter) theta.1=rep(1,num.iter) for( i in 1:(num.iter-1)){ B=c();V=c() # Sampling B,V for(j in 1:n){ if(Y[j]==0){ B[j]=rbern(1,p.1[i]) if(B[j]==1){V[j]=rpois(1,theta.1[i])} else{V[j]=0} } else{ B[j]<-0 V[j]<-Y[j] } } #Gibbs sampling p,theta p.1[i+1]=rbeta(1,sum(B)+b1,sum(1-B)+b2) theta.1[i+1]=rgamma(1,shape = sum(V)+a1,rate = n+a2) } # starting p=0.5 / theta = 2 p.2=rep(0.5,num.iter) theta.2=rep(2,num.iter) for( i in 1:(num.iter-1)){ B=c();V=c() # Sampling B,V for(j in 1:n){ if(Y[j]==0){ B[j]=rbern(1,p.2[i]) if(B[j]==1){V[j]=rpois(1,theta.2[i])} else{V[j]=0} } else{ B[j]<-0 V[j]<-Y[j] } } #Gibbs sampling p,theta p.2[i+1]=rbeta(1,sum(B)+b1,sum(1-B)+b2) theta.2[i+1]=rgamma(1,shape = sum(V)+a1,rate = n+a2) } # starting p=0.7 / theta = 3 p.3=rep(0.7,num.iter) theta.3=rep(3,num.iter) for( i in 1:(num.iter-1)){ B=c();V=c() # Sampling B,V for(j in 1:n){ if(Y[j]==0){ B[j]<-rbern(1,p.3[i]) if(B[j]==1){V[j]<-rpois(1,theta.3[i])} else{V[j]<-0} } else{ B[j]<-0 V[j]<-Y[j] } } #Gibbs sampling p,theta p.3[i+1]=rbeta(1,sum(B)+b1,sum(1-B)+b2) theta.3[i+1]=rgamma(1,shape = sum(V)+a1,rate = n+a2) } p=c(p.1[index],p.2[index],p.3[index]) theta=c(theta.1[index],theta.2[index],theta.3[index]) df.zip=data.frame("X1"=character(),"X1"=numeric(),"X1"=numeric(),"X1"=numeric(),"X1"=numeric(),"X1"=numeric()) #summaries for theta df.zip[1,]=cbind("theta",round(mean(theta),3), round(sd(theta),3), round(quantile(theta,0.025),3), round(quantile(theta,0.5),3), round(quantile(theta,0.975),3)) #summaries for p df.zip[2,]=cbind("p",round(mean(p),3), round(sd(p),3), round(quantile(p,0.025),3), round(quantile(p,0.5),3), round(quantile(p,0.975),3)) #summaries for mu mu=(1-p)*theta df.zip[3,]=cbind("mu",round(mean(mu),3), round(sd(mu),3), round(quantile(mu,0.025),3), round(quantile(mu,0.5),3), round(quantile(mu,0.975),3)) #summaries for P(Y=0) prob.z=p+(1-p)/exp(theta) df.zip[4,]=cbind("P(Y=0)",round(mean(prob.z),3), round(sd(prob.z),3), round(quantile(prob.z,0.025),3), round(quantile(prob.z,0.5),3), round(quantile(prob.z,0.975),3)) #summaries for deviance dev.zip=-2*log((p*exp(theta)+(1-p))^{sum(as.numeric(Y==0))}*(1-p)^{sum(as.numeric(Y>0))}*theta^{sum(Y)}*exp(-n*theta)) df.zip[5,]=cbind("Deviance",round(mean(dev.zip),3), round(sd(dev.zip),3), round(quantile(dev.zip,0.025),3), round(quantile(dev.zip,0.5),3), round(quantile(dev.zip,0.975),3)) colnames(df.zip)=c("","Mean","SD","2.5%","Median","97.5%") df.zip ################################################# #4.Y~ZINB(p,theta) #starting point r = 1,2,3 d.r=function(candi,t){ den=prod(choose(Y+candi-1,Y))*(1-t)^{(n+a2)*candi} return(den) } set.seed(0828) #sample.1 with starting point r=1 , theta=p=0.3 r.1=rep(1,num.iter) theta.1=rep(0.2,num.iter) p.1=rep(0.2,num.iter) for ( i in 1:(num.iter-1)){ B=c();V=c() # Sampling B,V for(j in 1:n){ if(Y[j]==0){ B[j]=rbinom(1,1,p.1[i]) if(B[j]==1){V[j]=rnbinom(1,r.1[i],theta.1[i])} else if(B[j]==0){V[j]=0} } else{ B[j]=0;V[j]=Y[j] } } # Do independet sampling for r candi.r=rdunif(1,1,15) u=runif(1) a=min((d.r(candi.r,theta.1[i])/ddunif(candi.r,1,15))/(d.r(r.1[i],theta.1[i])/ddunif(r.1[i],1,15)),1) if(u<=a){r.1[i+1]=candi.r} else{r.1[i+1]=r.1[i]} # Gibbs sampling for theta theta.1[i+1]=rbeta(1,sum(V)+a1,(n+a2)*r.1[i+1]+1) p.1[i+1]=rbeta(1,sum(B)+b1,sum(1-B)+b2) } #sample.1 with starting point r=2 , theta=p=0.5 r.2=rep(2,num.iter) theta.2=rep(0.5,num.iter) p.2=rep(0.5,num.iter) for ( i in 1:(num.iter-1)){ B=c();V=c() # Sampling B,V for(j in 1:n){ if(Y[j]==0){ B[j]=rbern(1,p.2[i]) if(B[j]==1){V[j]=rnbinom(1,r.2[i],theta.2[i])} else if(B[j]==0){V[j]=0} } else{ B[j]=0;V[j]=Y[j] } } # Do independet sampling for r candi.r=rdunif(1,1,15) u=runif(1) a=min((d.r(candi.r,theta.2[i])/ddunif(candi.r,1,15))/(d.r(r.2[i],theta.2[i])/ddunif(r.2[i],1,15)),1) if(u<=a){r.2[i+1]=candi.r} else{r.2[i+1]=r.2[i]} # Gibbs sampling for theta theta.2[i+1]=rbeta(1,sum(V)+a1,(n+a2)*r.2[i+1]+1) p.2[i+1]=rbeta(1,sum(B)+b1,sum(1-B)+b2) } #sample.1 with starting point r=3 , theta=p=0.7 r.3=rep(3,num.iter) theta.3=rep(0.7,num.iter) p.3=rep(0.7,num.iter) for ( i in 1:(num.iter-1)){ B=c();V=c() # Sampling B,V for(j in 1:n){ if(Y[j]==0){ B[j]=rbern(1,p.3[i]) if(B[j]==1){V[j]=rnbinom(1,r.3[i],theta.3[i])} else if(B[j]==0){V[j]=0} } else{ B[j]=0;V[j]=Y[j] } } # Do independet sampling for r candi.r=rdunif(1,1,15) u=runif(1) a=min((d.r(candi.r,theta.3[i])/ddunif(candi.r,1,15))/(d.r(r.3[i],theta.3[i])/ddunif(r.3[i],1,15)),1) if(u<=a){r.3[i+1]=candi.r} else{r.3[i+1]=r.3[i]} # Gibbs sampling for theta theta.3[i+1]=rbeta(1,sum(V)+a1,(n+a2)*r.3[i+1]+1) p.3[i+1]=rbeta(1,sum(B)+b1,sum(1-B)+b2) } r=c(r.1[index],r.2[index],r.3[index]) theta=c(theta.1[index],theta.2[index],theta.3[index]) p=c(p.1[index],p.2[index],p.3[index]) df.zinb=data.frame("X1"=character(),"X1"=numeric(),"X1"=numeric(),"X1"=numeric(),"X1"=numeric(),"X1"=numeric()) #summaries for 1-theta df.zinb[1,]=cbind("1-theta",round(mean(1-theta),3), round(sd(1-theta),3), round(quantile(1-theta,0.025),3), round(quantile(1-theta,0.5),3), round(quantile(1-theta,0.975),3)) #summaries for r df.zinb[2,]=cbind("r",round(mean(r),3), round(sd(r),3), round(quantile(r,0.025),3), round(quantile(r,0.5),3), round(quantile(r,0.975),3)) #summaries for p df.zinb[3,]=cbind("p",round(mean(p),3), round(sd(p),3), round(quantile(p,0.025),3), round(quantile(p,0.5),3), round(quantile(p,0.975),3)) #summaries for mu mu=r*theta*(1-p)/(1-theta) df.zinb[4,]=cbind("mu",round(mean(mu),3), round(sd(mu),3), round(quantile(mu,0.025),3), round(quantile(mu,0.5),3), round(quantile(mu,0.975),3)) #summaries for P(Y=0) prob.z=(p+(1-p)*(1-theta)^{r}) df.zinb[5,]=cbind("P(Y=0)",round(mean(prob.z),3), round(sd(prob.z),3), round(quantile(prob.z,0.025),3), round(quantile(prob.z,0.5),3), round(quantile(prob.z,0.975),3)) #summaries for deviance dev.zinb=-2*log((p*(1-theta)^{-r}+(1-p))^{sum(as.numeric(Y==0))}*(1-p)^{sum(as.numeric(Y==1))}*theta^{sum(Y)}*(1-theta)^{n*r}) df.zinb[6,]=cbind("Deviance",round(mean(dev.zinb),3), round(sd(dev.zinb),3), round(quantile(dev.zinb,0.025),3), round(quantile(dev.zinb,0.5),3), round(quantile(dev.zinb,0.975),3)) colnames(df.zinb)=c("","Mean","SD","2.5%","Median","97.5%") df.zinb
'Statistics > 논문 리뷰' 카테고리의 다른 글
| 밀도 기반 군집 방법 - DBSCAN (0) | 2022.03.10 |
|---|---|
| 보조 혼합 샘플링을 이용한 베이지안 로짓 모형(Bayesian logit models with auiliary mixture sampling) (1) | 2022.03.07 |
| ZIP and Binomial regression with Random effect_요약 정리 (0) | 2020.12.28 |
| Bayesian Approach for ZIP model _ 정리,예제 (2) | 2020.07.16 |




댓글